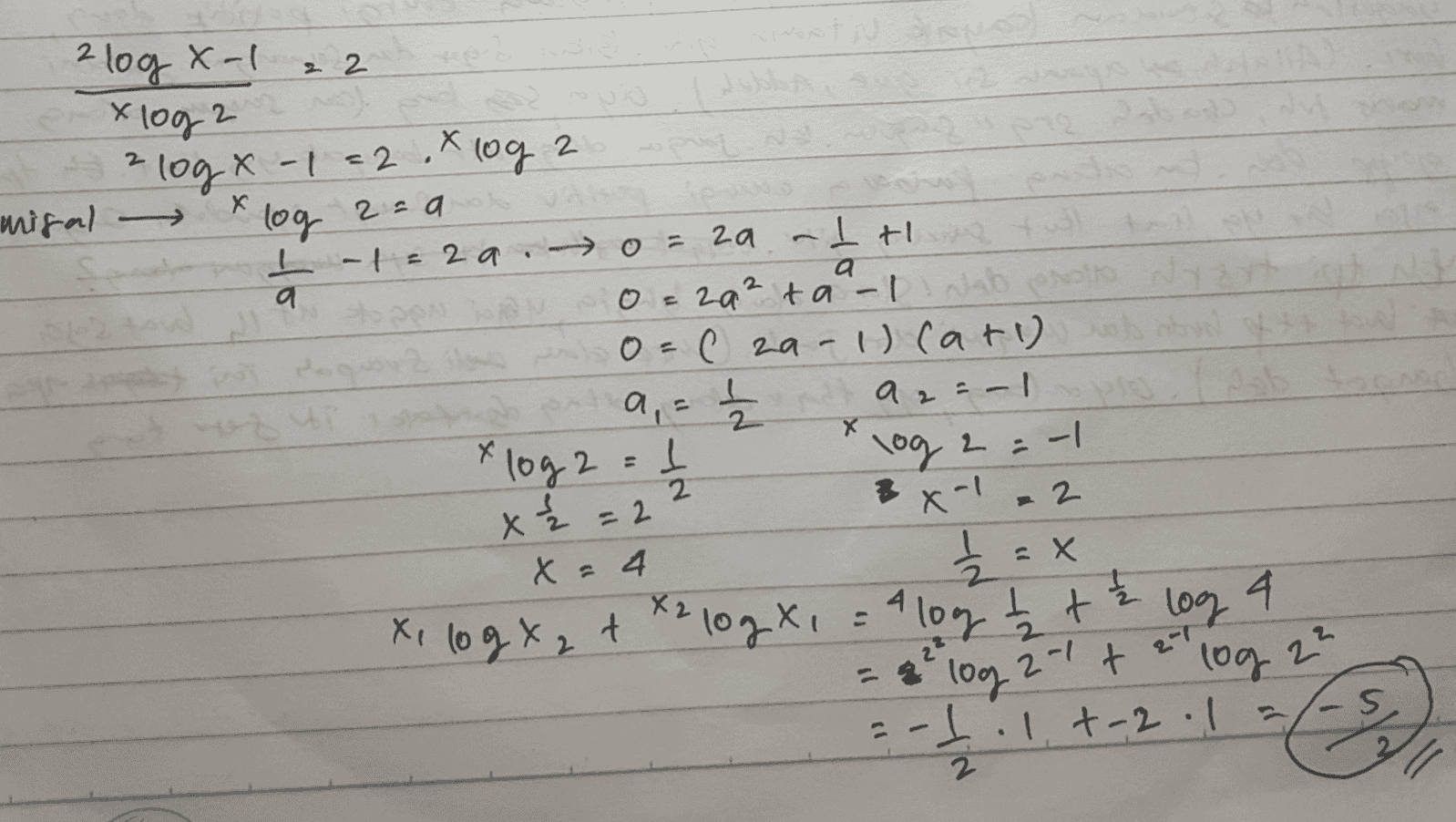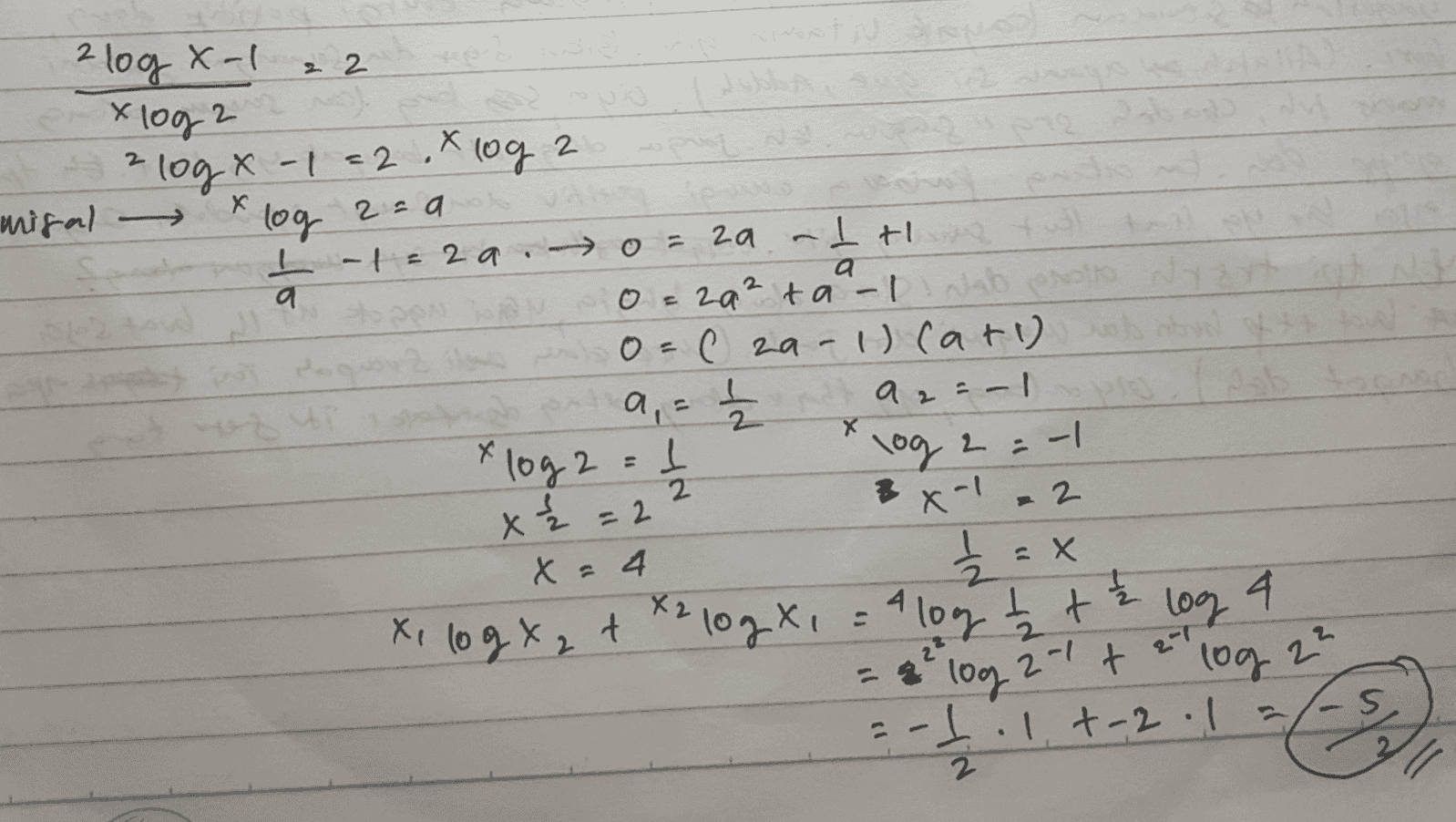Удиви меня

Logx 2 x2 2 2

Logx2. Logx/2 x2. Logx (3x^2+x-3)=3. Logx2 -1/x+2/x2. Logx+149 2.
Logx2. Logx/2 x2. Logx (3x^2+x-3)=3. Logx2 -1/x+2/x2. Logx+149 2.
Решите неравенство: log x 2 ( x + 1 ) 2 ≤ 1. Logx2 -1/x+2/x2. (log^2x-2logx)^2. Logx(2x-1). Logx2 -1/x+2/x2.
Решите неравенство: log x 2 ( x + 1 ) 2 ≤ 1. Logx2 -1/x+2/x2. (log^2x-2logx)^2. Logx(2x-1). Logx2 -1/x+2/x2.
Logx2-log4x2. Logx(2x-1). Log2 x=log2 3 2x-3. Logx 2 x2 2 2. Метод введения новой переменной логарифмические уравнения.
Logx2-log4x2. Logx(2x-1). Log2 x=log2 3 2x-3. Logx 2 x2 2 2. Метод введения новой переменной логарифмические уравнения.
Решите неравенство 𝑥3 + 2𝑥2 ≤ 3x. Logx(2x^2-3x+2)=2. Решите неравенство log x 2+x x 2-2x+1. Logx(2x-1). Logx 2 x2 2 2.
Решите неравенство 𝑥3 + 2𝑥2 ≤ 3x. Logx(2x^2-3x+2)=2. Решите неравенство log x 2+x x 2-2x+1. Logx(2x-1). Logx 2 x2 2 2.
Logx 5,2. Logx16=2. Logx(2x-1). X>2 неравенство. Logx 2 x2 2 2.
Logx 5,2. Logx16=2. Logx(2x-1). X>2 неравенство. Logx 2 x2 2 2.
Logx2. Logx 2 x2 2 2. Log2x-2logx2 -1. Logx+2(16)=4. Logx2.
Logx2. Logx 2 x2 2 2. Log2x-2logx2 -1. Logx+2(16)=4. Logx2.
Решите неравенство x 2 - 12x+36 > 0. Logx 2 x2 2 2. Logx x 2 logx x 2 меньше 0. Logx 2 x2 2 2. Гдз по алгебре 11 класс никольский потапов.
Решите неравенство x 2 - 12x+36 > 0. Logx 2 x2 2 2. Logx x 2 logx x 2 меньше 0. Logx 2 x2 2 2. Гдз по алгебре 11 класс никольский потапов.
2x 2 3x 2 0 решить неравенство. Logx 2 x2 2 2. Решите неравенство: log x ≤ 2. Logx 2 x2 2 2. Logx 2 x2 2 2.
2x 2 3x 2 0 решить неравенство. Logx 2 x2 2 2. Решите неравенство: log x ≤ 2. Logx 2 x2 2 2. Logx 2 x2 2 2.
Logx 2 x2 2 2. Лог 2 x> 1. Logx 2 x2 2 2. Logx+3(x + 2) · logx+2(x + 15) > 2,. Logx 2 x2 2 2.
Logx 2 x2 2 2. Лог 2 x> 1. Logx 2 x2 2 2. Logx+3(x + 2) · logx+2(x + 15) > 2,. Logx 2 x2 2 2.
Logx 2 x2 2 2. Logx2 -1/x+2/x2. Logx(2x-1). Log2(2x-1)=3 решение. Logx 2 x2 2 2.
Logx 2 x2 2 2. Logx2 -1/x+2/x2. Logx(2x-1). Log2(2x-1)=3 решение. Logx 2 x2 2 2.
Logx(2x-1). Logx16-logx2 1/2. Лог1/3 х>4. Logx 2 x2 2 2. Logx/2 x2.
Logx(2x-1). Logx16-logx2 1/2. Лог1/3 х>4. Logx 2 x2 2 2. Logx/2 x2.
Log 1/2 x. Logx 2 x2 2 2. Logx+1 2=log2 x+1. Logx2 -1/x+2/x2. Введение новой переменной логарифмических уравнений.
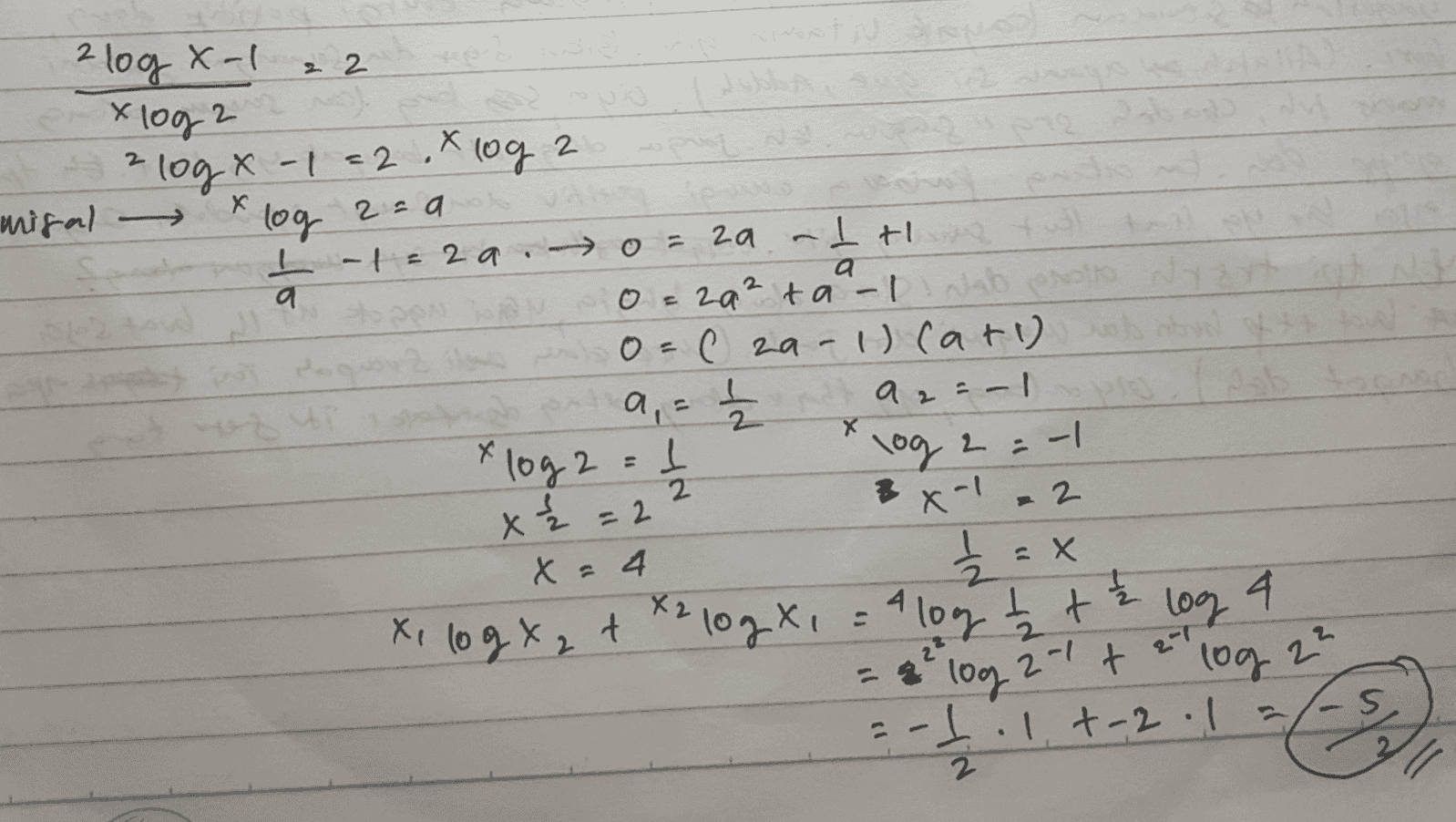Log 1/2 x. Logx 2 x2 2 2. Logx+1 2=log2 x+1. Logx2 -1/x+2/x2. Введение новой переменной логарифмических уравнений.
Logx+1(x^2+x). Logx^2+1(x-3)^2 logx^2+1((x-3)^2/(x^2+1)^3). Решите неравенство logx 2(x2 − 2x + 1) ≥ 2. Log3(x+1)+logx+1 3=2. Logx+2 (3x^2+x-5)=2.
Logx+1(x^2+x). Logx^2+1(x-3)^2 logx^2+1((x-3)^2/(x^2+1)^3). Решите неравенство logx 2(x2 − 2x + 1) ≥ 2. Log3(x+1)+logx+1 3=2. Logx+2 (3x^2+x-5)=2.
Решить уравнение log. Logx 2 x2 2 2. Logx2 x x2-2x 1. Logx 2 x2 2 2. Log2x=3.
Решить уравнение log. Logx 2 x2 2 2. Logx2 x x2-2x 1. Logx 2 x2 2 2. Log2x=3.
Решите неравенство logx(3x+1)>logx(x+2). Logx2 1 4log2 корень x. Logx (x2-2x-3)< logx1. Logx2+1 (x − 3)2 · logx2+1 (x − 3)2 (x 2 + 1)3 ⩽ −2. Logx 2 x2 2 2.
Решите неравенство logx(3x+1)>logx(x+2). Logx2 1 4log2 корень x. Logx (x2-2x-3)< logx1. Logx2+1 (x − 3)2 · logx2+1 (x − 3)2 (x 2 + 1)3 ⩽ −2. Logx 2 x2 2 2.
Log2(x)/log2(2x-1)<0. Log2(x+2) уравнение. Logx/2 x2. Logx2 -1/x+2/x2. Logx x-2 logx x+2.
Log2(x)/log2(2x-1)<0. Log2(x+2) уравнение. Logx/2 x2. Logx2 -1/x+2/x2. Logx x-2 logx x+2.
Logx 2 x2 2 2. Logx*logx. Logx x-2 logx x+2. Логарифмические уравнения log2/3 + log3. Log 1/2 x.
Logx 2 x2 2 2. Logx*logx. Logx x-2 logx x+2. Логарифмические уравнения log2/3 + log3. Log 1/2 x.
Logx 2 x2 2 2. Logx2 -1/x+2/x2. 2x 2 3x 2 0 решить неравенство. Logx(2x-1). Logx(2x^2-3x+2)=2.
Logx 2 x2 2 2. Logx2 -1/x+2/x2. 2x 2 3x 2 0 решить неравенство. Logx(2x-1). Logx(2x^2-3x+2)=2.
Logx(2x-1). Log3(x+1)+logx+1 3=2. Logx2 -1/x+2/x2. Метод введения новой переменной логарифмические уравнения. Logx (x2-2x-3)< logx1.
Logx(2x-1). Log3(x+1)+logx+1 3=2. Logx2 -1/x+2/x2. Метод введения новой переменной логарифмические уравнения. Logx (x2-2x-3)< logx1.
Logx2 -1/x+2/x2. Logx2 -1/x+2/x2. Решите неравенство x 2 - 12x+36 > 0. Log3(x+1)+logx+1 3=2. Logx2-log4x2.
Logx2 -1/x+2/x2. Logx2 -1/x+2/x2. Решите неравенство x 2 - 12x+36 > 0. Log3(x+1)+logx+1 3=2. Logx2-log4x2.